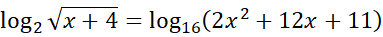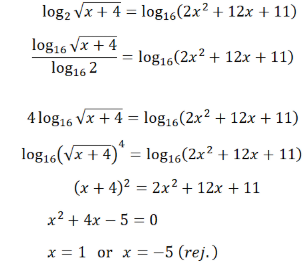【高中數學】DSE Logarithmic Functions 對數函數完全攻略

Logarithmic Functions 對數函數，簡稱【Log】，中四開始教Log可能睇落好深奧，但其實Log對數應用喺日常生活同科學領域都好常見！由地震強度、ph值到聲音分貝，全部都會運用到Log對數，同時都係 DSE 必考課題之一！今日Uni+用最淺白嘅方法，同大家拆解對數嘅基本概念同方程解題技巧，等你輕鬆應付到所有Log嘅題型！

Logarithmic Functions 對數函數基本概念

• 以下面例子理解 Log 對數嘅定義

如果 a^x = y，咁 log_a y = x，即係問：「要用 a 做底，計幾次方先可以得到 y？」

例子：2³ = 8，所以 log₂ 8 = 3

同學試想像：「如果我每日儲錢翻倍，要儲幾多日先可以有 8 蚊？」

• 第一日：2 蚊
• 第二日：4 蚊
• 第三日：8 蚊
• 答案係 3 日，即係 log₂ 8 = 3

考試必考！Log對數函數必記公式

下一步，同學不如試下用Emoji記下Log對數函數必考公式！

1. log_a m + log_a n = log_a (mn)
   log✋ + log🤚 = log✋🤚
2. log_a m − log_a n = log_a (m / n)
   log🐥 − log🥚 = log🐣
3. log_a (mⁿ) = nlog_a m
   log😅 = 💧log😄
4. log_a 1 = 0
5. log_a a = 1
6. log_a b = log_c b / log_c a

方程解題技巧四大題型

第一題型：未知數喺次方

例題： 3^x = 8

解法：

3^x = 8

log 3^x = log 8

x · log 3 = log 8

x = log 8 / log 3

x ≈ 1.89

第二題型：單邊有log

例題： log₅(3x + 4)   +  log₅(x − 2) = 3

解法：

log₅(3x + 4) + log₅(x − 2) = 3

    log₅[(3x + 4)(x − 2)] = 3

       (3x + 4)(x − 2) = 5³

       3x² − 2x − 133 = 0

         x = 7  或  x = − 19 / 3 (rej.)

第三題型：兩邊都有log

記住： log A = log B ⇔ A = B

例題： log(5x + 2) − log(x + 1) = log 4

解法：

log(5x + 2) − log(x + 1) = log 4

          log[(5x + 2)/(x + 1)] = log 4

                (5x + 2)/(x + 1) = 4

                5x + 2 = 4x + 4

                       x = 2

第四題型：唔同底數

小提醒！轉換做相同底數先計！

例題:

解法:

考試貼士

Q：做題有咩注意事項？

A：答題時有以下4個注意：

1. 檢查定義域(x > 0)

   對數函數嘅定義域係 x > 0，即輸入值必須大於 0。

   解題時要注意呢個限制，唔可以出現負數或 0 嘅情況。

2. 小心底數限制 (a > 0 且 a ≠ 1)

   對數函數嘅底數 a 必須滿足 a > 0 且 a ≠ 1。

   唔能夠使用 a = 0 或 a = 1 嘅情況，否則會出現問題。

3. 記得驗證答案

4. 揀走不合理答案

   有時可能會得出多個答案，要根據題目條件和對數函數嘅性質，排除不符合要求的答案。

Q：Log做題有咩常見陷阱？

A：大概整理到以下5點！大家要小心啊！

1. 忽略底數

   係使用對數函數時，要注意底數係咩，唔能夠混淆唔同底數嘅對數。

   例如:log(100) 和 log2(100) 係唔同嘅結果。

2. 未驗證最終答案

   係解題過程中，要注意最終得出嘅答案是否合理，例如:如果最後計算出 log2(8) = 4，就要仔細檢查係咪有錯誤。

3. 忽略對數嘅性質

   對數函數有一些重要嘅性質,如 log(xy) = log(x) + log(y)。

   係解題時要善用呢d性質,否則容易出錯。

4. 處理小數或負數

   對數函數係處理小數或負數時需要特別注意。

   例如:log(-2) 係無意義的,需要先判斷是否合理。

5. 混淆指數函數和對數函數

   指數函數和對數函數係相反嘅操作，但係解題時容易混淆。

   要清楚區分兩者嘅定義和性質。

必勝錦囊

• 記住對數和指數關係

  係對數同指數係互逆運算

  記住「底、指、數」三個位置嘅關係

  做對數題目時，可以轉換成指數形式去諗

• 遇到複雜題目,分步驟慢慢來

• 寫清楚每一步，唔好跳Step

  係解題過程中,要詳細地記錄每一步推導過程，Marking都有過程分架！

• 最後一定要驗證答案

  就算解題過程望落正確，都要final check！

記住：「熟能生巧」，只要多練習，Log一定冇難度！

皇牌數學常規課程

Uni+ Education 提供中一至中六的數學補習班，課程由多位大學數學系本科畢業，包括港大，科大等，實戰考獲5*以上佳績，真正實力保證！本中心採用小班教學形成，師生比例1：8，貼心照顧同學的學習需要！

導師團隊亦會撰寫不同Revision Set溫習筆記，更設計出大量獨家試題練習及模擬試卷，幫助學生避開常見陷阱，輕鬆命中Marking Scheme！同時設有課後問書服務，幫助不同程度學生

持續進步，考獲理想佳績！

課程資訊
每星期一至兩堂
每堂1小時15分鐘
上課地點
香港佐敦吳松街191號突破中心1/F及6/F全層
​合適同學
中一至中六想加強數學科的同學
費用
 $330/堂