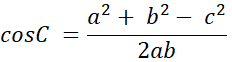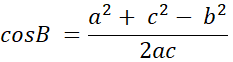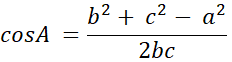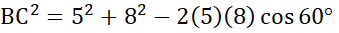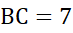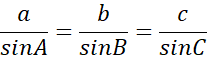【高中數學】Application of Trigonemetry 三角學的應用: Cosine Formula餘弦 與 Sine Formula正弦定理完整指南
點解要學三角學公式?三角學公式係數學科DSE入面一個好重要嘅課題,雖然公式睇落好多,但其實都係有規律。今日等Uni+同大家拆解餘弦定理Cosine Formula同正弦定理Sine Formula嘅規律同精髓,等你輕鬆應付DSE!
第一部分:Cosine Formula 餘弦定理詳解
1.Cosine Formula的基本形式
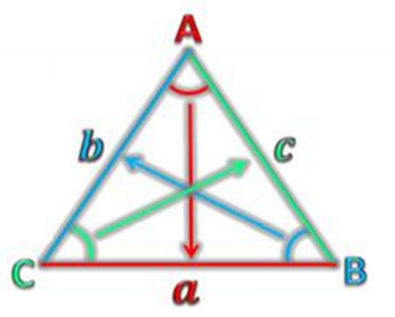
在任意三角形ABC中:
c² = a² + b² - 2ab·cosC
b² = a² + c² - 2ac·cosB
a² = b² + c² - 2bc·cosA
2. 求角度的變形公式
3. 應用場景例子
已知三邊求任一角
已知兩邊及其夾角求第三邊
不限於直角三角形
4. 實例解析
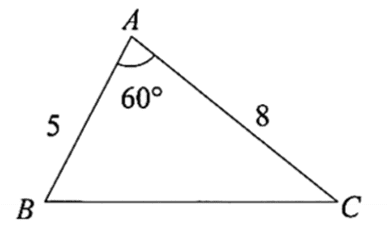
例題:在三角形ABC中 AB=5,AC=8,∠BAC=60°,求 BC。
解答步驟:
1. 使用餘弦定理:
2.
3.
第二部分:Sine Formula 正弦定理詳解
1. Sine Formula的公式
2. 應用場景
已知一邊兩角
已知兩邊一角(注意可能有兩解)
不限於直角三角形
3. 實例解析
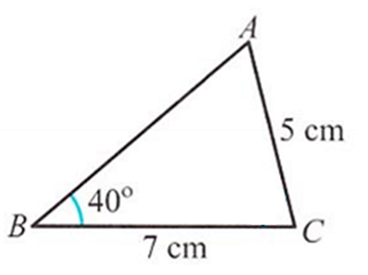
例題:在三角形ABC中 AC=5,BC=7,∠ABC=40°,求 ∠BAC。
解答步驟:
1.使用正弦定理:
2.
3.
4.
或
(兩者皆有可能,因加上仍小於 )
第三部分:兩定理的比較
| Cosine Formula 餘弦定理特點 | Sine Formula 正弦定理特點 |
|---|---|
| 已知三邊求角度 | 已知一邊兩角 |
| 已知兩邊一角求第三邊 | 已知兩邊一角 (小心可能有兩個答案!) |
| 唔限直角三角形 | 唔限直角三角形 |
📌 考試必勝貼士
Q:見到題目究竟要揀邊個Formula?
A:睇下題目提供已知數據:
有三邊 ➡️ Cosine Formula
有多角度 ➡️ Sine Formula
Q:三個常見陷阱 ⚠️
A:要留意以下三點:
唔好漏咗第二個答案
要驗證答案是否合理
角度加埋唔可以大過180°
希望呢篇文章能夠幫到大家!記住三角學唔係背公式咁簡單,最緊要係理解同練習。只要肯付出時間,一定可以喺DSE數學科攞到好成績!
皇牌數學常規課程
Uni+ Education 提供中一至中六的數學補習班,課程由多位大學數學系本科畢業,包括港大,科大等,實戰考獲5*以上佳績,真正實力保證!本中心採用小班教學形成,師生比例1:8,貼心照顧同學的學習需要!
導師團隊亦會撰寫不同Revision Set溫習筆記,更設計出大量獨家試題練習及模擬試卷,幫助學生避開常見陷阱,輕鬆命中Marking Scheme!同時設有課後問書服務,幫助不同程度學生持續進步,考獲理想佳績!
課程資訊
每星期一至兩堂
每堂1小時15分鐘
上課地點
香港佐敦吳松街191號突破中心1/F及6/F全層
合適同學
中一至中六想加強數學科的同學
費用
$330/堂