圓形基本性質｜Basic Properties of Circles

「圓的基本性質Basic Properties of Circles」是數學DSE的考核範圍，亦是相對較難的課題，同學除了要熟習圓面積、直徑半徑的計算外，亦要知道切線、半徑、直徑、圓形內接三角形或四邊形、弦弧線之間的關係等，今次 UNI+為大家整合出最詳細的 Basic Properties of Circles，幫你輕鬆奪星！

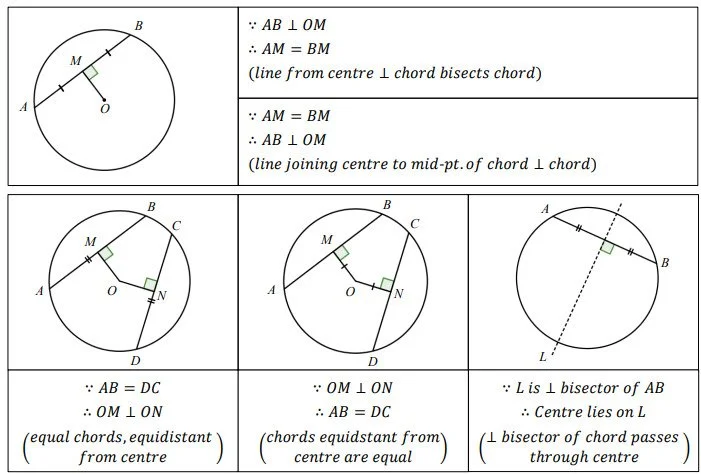
圓心與弦的關係 (Perpendiculars to Chords)

1. 弦的垂直平分線必經圓心(⊥bisector of chord passes through centre）

定理：任何一條弦的垂直平分線必定通過圓心。

2. 圓心至弦的垂線會平分弦(⊥from centre to chord bisects chord）

定理：在一個圓形內，如果由圓心向一條弦作垂線，這條垂線必定平分該弦。

3. 圓心連接弦中點的線段垂直於弦 (line joining centre and mid-pt. of chord ⊥chord)

定理：若將圓心與弦的中點連接，所得的線段會垂直於該弦。

4. 等弦與圓心等距(eq. chords equidistant from centre)

5. 與圓心等距的弦等長(chords equidistant from centre eq.）

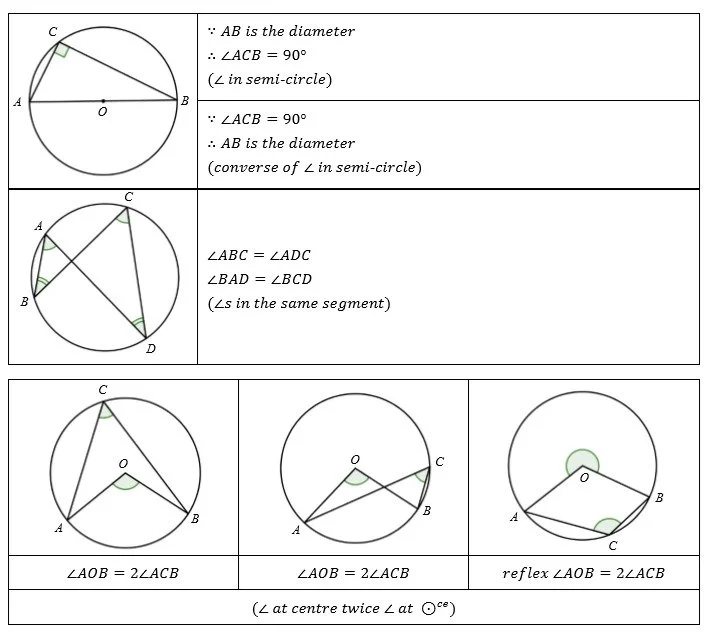
圓形的角性質 (Angles in Circle)

1. 同弓形內的圓周角相等(∠s in the same segment)

定理：在同一弧段上，不論選取哪兩點構成圓周角，所形成的角度大小都相同。

*注意：此定理僅適用於同一弧段，而非整個圓周。

2. 圓心角是圓周角的兩倍(∠ at centre twice ∠ at circumference)

定理：在圓形中，若圓心角與圓周角對應於同一段弧，則圓心角的大小是圓周角的兩倍。

【此性質常用於推算弧長、扇形面積等幾何問題。】

3. 半圓上的圓周角為直角(∠ in semi-circle）

定理：若圓上的一條弦為直徑，則由該弦所對應的圓周角恆為 90°。

逆定理：若某個圓周角為直角，則它必然對應於圓的一條直徑。

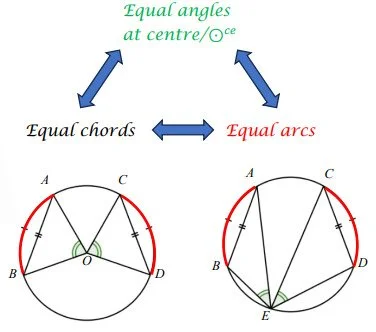
角、弧與弦的相等關係 (Equal Relations among Angles, Arcs and Chords)

在圓形內，角度、弧和弦之間存在緊密聯繫，主要有以下幾點：

1. 等角對等弧 / 等弧對等角 (equal arcs, equal ∠s)

2. 等角對等弦 / 等弦對等角 (equal chords, equal ∠s)

3. 等弦對等弧 / 等弧對等弦 (equal arcs, equal chords)

4. 弧與圓心角成比例 (arcs prop. to s at centre)

5. 弧與圓周角成比例 (arcs prop. to s at centre)

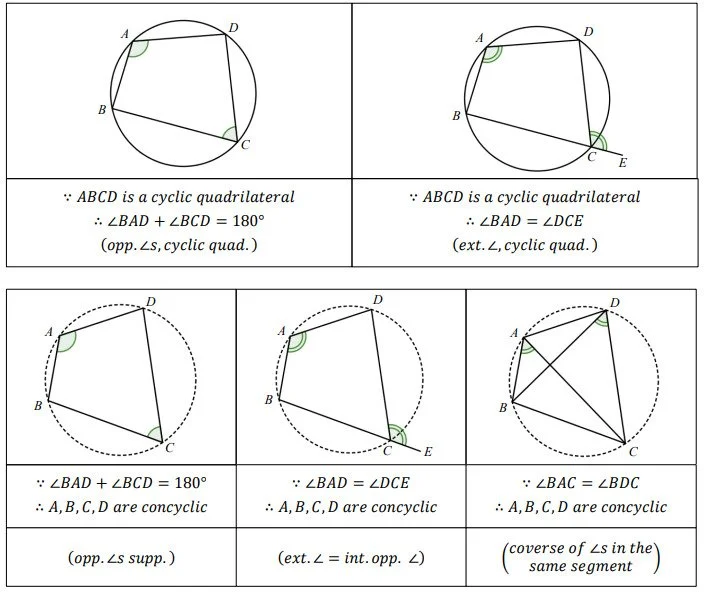
圓形內接四邊形（Cyclic quadrilateral）

1. 圓內接四邊形對角 (opp.∠s, cyclic quad.)

2. 圓內接四邊形外角(ext.∠s, cyclic quad.)

3. 同弓形內的圓周角的逆定理(Converse of ∠s in the same segment)

4. 對角互補 (opp.∠s supp)

5. 外角=內對角 (ext.∠ = int. opp.∠)

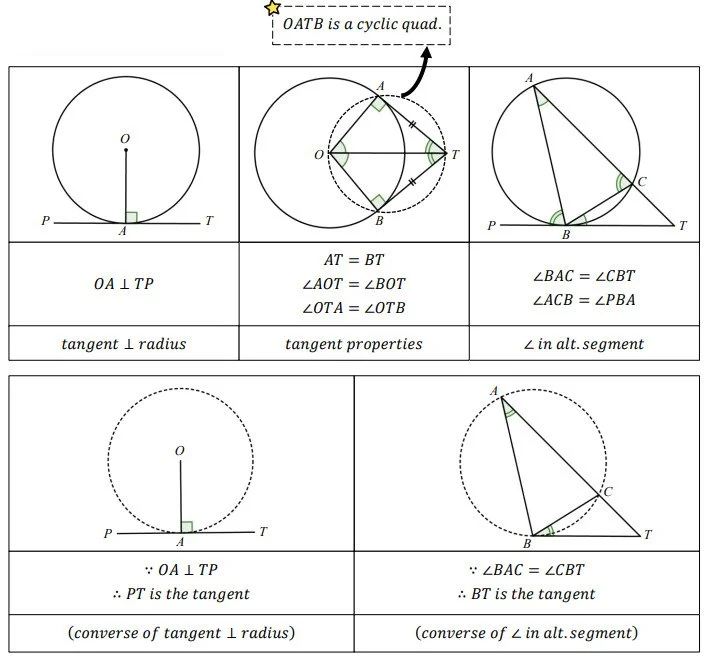
圓形與切線（Tangents to Circles）

1. 切線⊥半徑 / 切線⊥半徑的逆定理 (tangent ⊥ radius)

2. 切線性質 (tangent properties)

3. 交錯弓形上的圓周角 / 交錯弓形上的圓周角的逆定理 (∠ in alt. segment)

想學埋其他圓形嘅概論同圓的定理？相信UNI+嘅其他內容一定幫到你！想DSE數學拎高分，一定要多睇多計，記得Mark實UNI+，包你DSE數學摘星！

Uni + 皇牌數學常規課程（S1-S6）

想搵數學補習？Uni+ 的S1-S6皇牌數學常規課程，由多位數學系本科畢業導師團隊組成，包括香港大學，科技大學，中文大學等，並實戰考獲5*以上佳績，真正實力保證！課程會提供大量數學Mock Papers、獨家試題、模擬試、精讀筆記等，無論想奪星、補底，都能幫助學生達成理想成績目標！