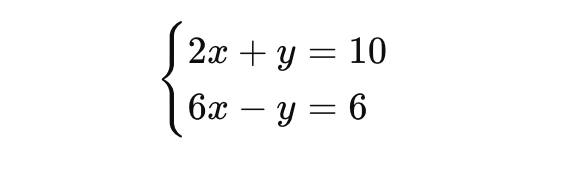秒懂聯立方程式(Simultaneous Equations)| 附必入聯立方程program!
聯立方程(Simultaneous Equations)是數學DSE必修課題,除了要將二元一次方程聯立得出兩個項數解,部分進階題目更要求同學更將概念應用到三元一次方程,再得出三個項數解,今次 UNI+為大家整合出最詳細的聯立方程投巧,幫你輕鬆奪星!
二元一次聯立方程式(Simultaneous Linear Equations)
「二元一次聯立方程式」是指有兩個未知數(例如:𝑥和𝑦),而且每條方程式都是一次方程(次方不大於1),我們要將兩條方程並列並找出兩個未知數的解,而數學上會用「 { 」來表示二元一次聯立方程式,以下是題目例子:
解二元一次聯立方程式(Simultaneous Linear Equations Solver)
代入消去法
「代入消去法」,是將其中一條方程的一個未知數用含另一個未知數的式子表示,再代入另一個方程,這樣就剩下一個未知數,就可以求得這個二元一次方程組的解,以下是常見例子:
解下列二元一次聯立方程式:
3x + 2y = 12
x − y = 1
解 :
3x + 2y = 12 …………(1)
x − y = 1 …………(2)
由(2)可得 x =1 + y 將其代入(1),我們可得:
3(1 + y )+2 y =12
3 + 3 y +2 y =12
5 y =12 - 3
y = 1.8
將 y =1.8 代入(2),我們可得: x - (1.8) = 1
x =2.8
故 x =2.8 , y =1.8 為二元聯立方程組的解。
加減消去法
加減消去法是透過加法、減法、乘除法,令兩條方程式其中一個未知數的係數相同,然後把其中一個未知數「消去」,再求出另一個未知數,以下是是常見例子:
解下列各二元一次聯立方程式:
2x + y = 10
6x - y = 6
解 :
2x + y = 10 …………(1)
6x - y = 6 …………(2)
將 (1) 和 (2) 相加,可得:
(2x + y) + (6x − y) = 10 + 6
8x = 16
x = 2
再將 x = 2 代入 (1) ,可得:
2 (2) + y = 10
y = 6
故 x = 2, y = 6 為二元聯立方程組的解。
代入消去法和加減消去法哪個解法比較好?
觀察題型的時候,如果可以很明顯的觀察到 x = ? 或者 y = ? 時,那就可以使用代入消去法來解決這個題型;而如果兩個方程式的未知數的係數,是相同數字或相反數,這個時候使用加減消去法會比較好。
| 代入消去法 | 加減消去法 |
|---|---|
|
✅ 可以清楚地知道 x = ? 或 y = ? ✅ 未知數的係數為 1 時,較推薦使用 |
✅ 兩個方程式的係數,是相同數字或相反數 ✅ 係數不為 1,且數字不大 |
三元一次方程(linear equation with three unknowns)
圓方程三點求圓(Equation of Circle from 3 Points)
圓形方程的基本式為x2 + y2 + Dx + Ey + F = 0,然而如果要透過三點計算圓方程,就需要用到標準式:(x - a)2 + ( y - b )2 = r2
當中 x 同 y 為圓心嘅 x 座標 及 y 座標,a 同 b 為圓線上任意一點的 x 座標 及 y 座標,r 就是圓線上任意一點與圓心之間的距離,亦即半徑。
【例子】:
圓經過三點 (2,0),(0,1) 及 (0,4),求圓心, 半徑及圓的方程。
解 :
要解這個問題,我們可以使用圓的標準方程式 (x-a)2 + (y-b)2 = r2,其中 (x,y) 是圓心的坐標,(r) 是半徑。我們將這三個點分別代入方程式,然後解聯立方程組來找到 (x)、(y) 和 (r)。
給定的點是 (2,0),(0,1),和 (0,4)。代入這些點,我們得到三個方程:
1. 將 (2,0) 代入方程式得到 (x-2)2 + (y-0)2 = r2
2. 將 (0,1) 代入方程式得到 (x-0)2 + (y-1)2 = r2
3. 將 (0,4) 代入方程式得到 (x-0)2 + (y-4)2 = r2
接下來,我們將這三個方程簡化並解聯立方程組。
1. (x-2)2 + (y-0)2 = r2 變為 x2 + 4 - 4x + y2 = r2
2. (x-0)2 + (y-1)2 = r2 變為 x2 + 1 - 2y + y2 = r2
3. (x-0)2 + (y-4)2 = r2 變為 x2 + 16 - 8y + y2 = r2
現在我們解這個方程組找到 (x)、(y) 和 (r)。
首先,我們可以用 Equation 2 減去 Equation 1,消去 r2:
(x2 + 1 - 2y + y2) - (x2 + 4 - 4x + y2) = 0
簡化為: 4a - 2b = 3…………(4)
接下來,我們可以用 Equation 3 減去 Equation 2,同樣消去 r2:
(x2 + 16 - 8y + y2) - (x2 + 1 - 2y + y2) = 0
簡化為: 6b = 15…………(5)
解這個聯立方程組,得到 (x = 2) 和 (y = 2.5)。
最後,將 (x) 和 (y) 的值代入其中一個方程,例如 Equation 1:
22 + 4 - 4(2) + (2.5)2 = r2
得到 (r2 = 6.25),解得 (r = 2.5)。
因此,圓心是 (2, 2.5),半徑是 (2.5),圓的方程是 (x-2)2 + (y-2.5)2 = 6.25。
*注:一般式為 x2 − 4x + y2 − 5y + 4 = 0
聯立方程 program((二元一次方程)
步驟1. 先在 Mode 選擇中選擇 Mode 1
步驟2. 輸入相應數字到計數機中:
?→A:?→B:?→C:?→D:?→X:?→Y:(YB—CX)÷(DB—AX→X」B-1(C—AAns→Y
例子
{ 2x + y = 10
{ 6x - y = 6
計數機輸入:2,1,10,6,-1,6
答案: x=2, y=6
想學埋其他聯立方程的解法?相信UNI+嘅其他內容一定幫到你!想DSE數學拎高分,一定要多睇多計,記得Mark實UNI+,包你DSE數學摘星!
Uni + 皇牌數學常規課程(S1-S6)
想搵數學補習?Uni+ 的S1-S6皇牌數學常規課程,由多位數學系本科畢業導師團隊組成,包括香港大學,科技大學,中文大學等,並實戰考獲5*以上佳績,真正實力保證!課程會提供大量數學Mock Papers、獨家試題、模擬試、精讀筆記等,無論想奪星、補底,都能幫助學生達成理想成績目標!